新闻资讯 News

如果用光谱辐射计来考察各种辐射源的光谱分布，可明显地看出，存在两类完全不同的辐射源。如果辐射源是灼热固体或液体，则光谱分布曲线是连续的，仅有一个最大值，其波长随辐射源温度而变化，这种辐射源称为热辐射体。若辐射源是火焰或气体中的电气放电，则光谱分布曲线是不连续的，此时辐射通量集中在狭窄的光谱区间。用高分辨率的单色仪可以发观，这些区间十分挟窄．陡峭得象一条线．故这种分布称为线谱。另外，光谱也可以由狭窄的的线带组成，这种情况称为带谱。具有线谱或带谱的辐射源，称为选择性辐射体。初看起来，通量集中的所在波长在整个频谱上的位置似乎是杂乱的。详细的考察表明；它们表征了一定类型的辐射原子和分子的特性。因而，这些波长构成了辐射源独有的特征：线谱是原子的特征，带谱是分子的特征。

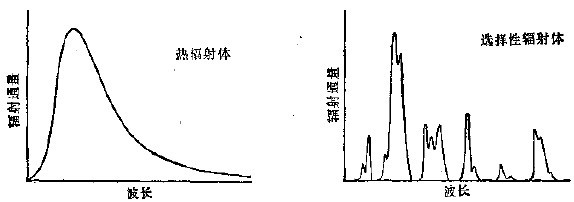
图1.9 热辐射体和选择性辐射体的光谱分布

红外系统设计者可能碰到的一些选择牲辐射体有：喷气发动机或火箭排出的热气流．再入大气层物体周围的激波受激层，以及通汛系统所用的气体放电源。典型的热辐射体有；喷气发动机发火箭尾喷管的热金属、气动加热表面、汽车、人．大地、空间飞行器以及天体。由于热辐射体远为普遍，因此，首先讨论一下适用于这些辐射源的定律。

比辐射率和基尔霍夫定律

19世纪后半期，物理学家一直在试图解释热辐射体的光谱能量分布。1860年，基尔霍夫在研究辐射传输的过程中发现：在任一给定的温度下，辐射通量密度和吸收系数之比，对任何材料都是常数。用一句精练的话表达，即：“好的吸收体也是好的辐射体”。

基尔霍夫还提出用“黑体”这个词来说明能吸收全部入射辐射能量的物体，按照他的定律，黑体必然是最有效的辐射体。因而，黑体是一个比较标准，它是任何其它辐射源可以与之进行比较的最有效的辐射体。一个辐射源的比辐射率即是指它的辐射能力与黑体发射能力之比。

从能量守恒角度很容易理解基尔霍夫定律。如果，我们将物体A1、A2放在恒温容器内，令容器内部为真空，则物体与容器之间及物体与物体之间只能通过辐射和吸收来交换能量。当系统达到热平衡时，所有物体与容器的温度相等，均为同一温度T。但是，物体A1和A2的表面情况不一样，它们所辐射出去的能量也不一样。显然，只有当辐射能量多的物体吸收能量也多时，才能和其他物体一样保持温度T不变。这就说明：物体的辐射出射度和吸收率之间存在一定的比例关系。

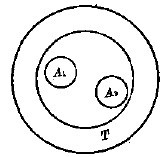
图1.10从能量守恒角度看基尔霍夫定律

基尔霍夫定律可用数学公式表达为：

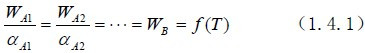
这里W_B为黑体（α_B=1）在温度T时的辐射出射度。

我们将比辐射率定义为辐射源的辐射出射度与具有同一温度的黑体的辐射出射度之比。即：

比辐射率是一个比值，其值介于非辐射源的零和黑体的1之间，可用来度量辐射源接近黑体的程度。代入基尔霍夫定律（1.4.1），可得到比辐射率和吸收率的关系：

结论：在给定温度下，任何材料的比辐射率在数值上等于该温度时的吸收率。

基尔霍夫定律对所有波长的全辐射是正确的，对波长为λ单色辐射也成立。

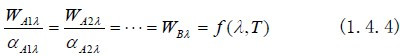
对波长为λ单色辐射，同样可定义光谱比辐射率，并得到：

例如：地球大气中有一层稳定的二氧化碳气体，它在14～16微米有一很强吸收带，也是14～16微米很稳定的强辐射源。卫星红外地平仪的探测波段就选择在14～16微米，实际探测的是稳定的二氧化碳大气层的辐射，而不是地球大地的辐射。这样可消除地球大地的辐射不均匀对姿态控制精度的影响。

普朗克热辐射定律

1879年，斯蒂芬从他的实验测量中得出结论：黑体辐射的总能量与它的绝对温度的四次方成正比。1884年，波尔兹曼应用热力学的关系也得到同样的结论；这个结果就是熟知的斯蒂芬－波尔兹曼定律。1894年，维恩发表位移定律，给出了黑体辐射光谱分布的一般形式，遗憾的是它仅与低温时短波段的实验数据相符。然而，他的位移定律，即温度与辐射能量峰值波长关系的距离仍然有效。1900年，瑞利基于经典物理的概念，推导出与高温时长波段实验数据相吻合的表达式，可是表达式预言能量随波长减小会无限制增加，被人称为“紫外灾难”。

1900年，普朗克发表的辐射定理，用量子物理的新概念补充了经典物理理沦，完整叙述了黑体辐射的光谱分布。普朗克定理可表示为:

通常也可写成：

温度从500°K到900°K范围的黑体辐射光谱通量密度曲线如图所示。这是一个重要范围，因为它包括了涡轮喷气机尾喷管的温度。

图1.11各种温度下的黑体光谱辐射通量密度

全光谱的辐射通量密度与光谱分布曲线下的面积相对应，可积分求解：

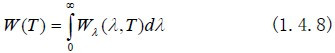
由图可见：随黑体温度增加，总辐射通量密度迅速增加，光谱辐射的峰值波长随向短波方向移动。另外，不同温度的光谱分布曲线彼此不相交，说明任何波长的光谱通量密度都随温度的升高而增加。

波段的辐射通量密度也可用同样方法求得，只是积分限不同：

可借助黑体辐射表计算波段辐射通量密度，由于黑体辐射表给出的是0～λ的辐射通量密度，可作变换求得结果：

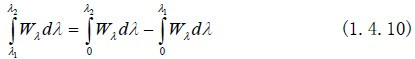
例如：热成象系统经常要用到常温（300°K）的黑体在8～14微米的辐射功率密度，可有：

随计算机技术的发展，用数值积分方法计算黑体辐射已不是难事。

斯蒂芬-波耳兹曼定律

在从零到无穷大的波长范围内,对普朗克光谱分布函数积分,可得黑体辐射到半球空间的辐射通量密度：

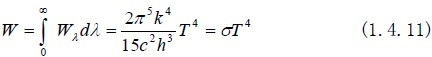
式中σ: 斯蒂芬-波耳兹曼常数, 5.6697×10^-12（W·cm^-2·K^-4）

辐射通量密度与绝对温度的四次方成正比。因此，相当小的温度变化，就会引起辐射功率密度很大的变化。

维恩位移定律

普朗克光谱分布函数对求波长的偏微分，并令其为零，可得出黑体的光谱辐

射通量密度的峰值波长 λ_m  和黑体绝对温度T 之间满足：

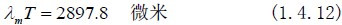
在实际可以达到的温度范围内, 光谱辐射的峰值波长均位于红外区域。如300K室温条件下，峰值波长为9.66微米，因此，8至14微米红外波段有时也称为热红外波段。

峰值波长的光谱辐射通量密度与绝对温度的五次方成正比，即：

式中b为1.2862×10^-15（W·cm^-2·Sr^-1·μ^-1·K^-5）

微分辐射亮度

我们将单位温差产生的黑体辐射亮度差称为微分辐射亮度，有的书上也称辐射对比度。

微分辐射亮度与红外系统的温度灵敏度关系十分密切。根据一幅红外热图像中目标和背景辐射亮度的差别，我们可以区分船只与水面、车辆与道路、庄稼与草地、建筑物与地面等。实际上，目标和背景之间温度差和比辐射率差都能产生两者的辐射对比度。为便于评估，红外热成像系统的探测灵敏度可用温度灵敏度的形式表达。如用：等效噪声温差（NEDT）、最小可分辨温差（MRDT）等。知道了热成像系统的温度灵敏度，由于比辐射率引起辐射对比度完全可用等效折算方法求得。

微分辐射亮度同样有光谱值和波段值之分，先介绍光谱微分辐射亮度。

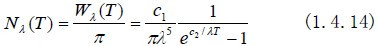
则光谱微分辐射亮度（单位：W·cm^-2·Sr^-1·μ^-1·K^-1）为

光谱微分辐射亮度是温度、波长的函数，在峰值波长λ_c处取得最大。对单位温差变化，波长为λ_c辐射的亮度差最大，对探测最为有利。光谱微分辐射亮度的峰值波长与温度之积也是常数，可表示为：

对照维恩位移定律，光谱微分辐射亮度达到最大的峰值波长λ_c不再是光谱辐

射出射度达到最大的λ_m，λ_c  小于λ_m 。

对于300K 的温度，λc  等于8 微米，峰值波长λm  为9.66 微米。后面将

讲到，地球大气层不是对所有波长都透过的，主要的大气窗口位于2 到2.5 微米,

3 到5 微米和8 到13 微米。8 到13 微米是热像仪观察地面目标最理想的工作波

段。无论是光谱辐射量,还是光谱辐射量随温度的变化率均较其他两个窗口高得

多。

光谱微分辐射亮度在工作波段的积分值叫做微分辐射亮度：

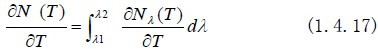
例1：计算室温墙面(300K)和人的皮肤（305K）在8～14微米的辐射出射度,忽略比辐射率的影响。

可用两种方法：

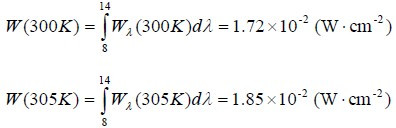
2) 利用300K时的出射度和微分辐射亮度计算

     300K时8～14微米波段的微分辐射亮度：

305K皮肤的辐射出射度：

温差较小时，两种方法算得结果近似相等。

例2：如一个8～14微米波段热象仪的300K室温时的温度灵敏度为0.1K，试估算如用来探测浮冰，或高压电缆接头，温度灵敏度将是多少？

可分别计算300K室温，273K浮冰及350K（设温升50度）的微分辐射亮度：

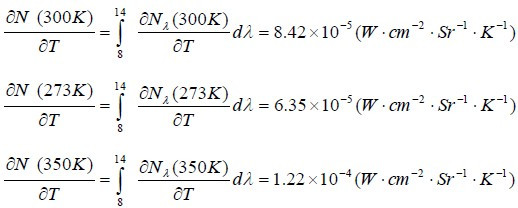
室温时的温度灵敏度为0.1K的热像仪，如探测浮冰，温度灵敏度为0.13K,如用来检测电缆接头是否过热，温度灵敏度可达0.07K。红外系统的温度灵敏度与被测物温度有关。