点源产生的辐照度
假设: 点源辐射强度为J ;点源到被照面元dA 的距离为ι; 面元法线与入
射光线的夹角为Θ 。
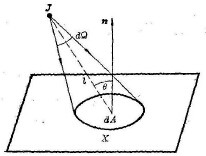
图1.6 点源产生的辐照度
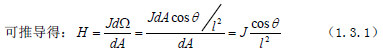
式中dΩ为点源对面元所张的立体角。
由式可见,在不考虑辐射传输损失时,点源产生的辐照度与距离平方成反比。其原因是:尽管点源的辐射强度不变,点源对系统所张的立体角随距离增加而减小。当辐射源未充满测量系统的视场覆盖时,系统测得的辐射数据与距离等测量条件有关,不能反映辐射源的真实情况。
根据式(1.2.3),仪器接收到的辐射通量取决于它的接收面积和接收立体角,而仪器的接收面积与它的有效孔径有关,接收立体角与系统视场有关。因此,有效孔径及视场是仪器最基本的参数。
对面源来讲,当测量距离确定后,由于仪器视场的限制,源发射面积中只有部分是有效的。由于有效孔径的限制,源向空间发射的能量只有落在有限的立体角内的部分能被系统所接收。
假设
dA2:仪器入瞳面积;
Θ2:dA2法线与测量方向的夹角;
dΩ2:仪器视场立体角;
dA1:面源有效发射面积;
Θ1:dA1法线与测量方向的夹角;
dΩ1:面源发射立体角
l:测量距离
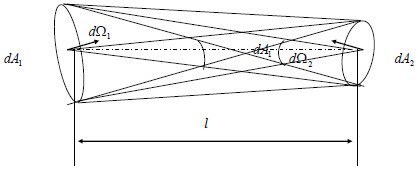
图1.7 封闭光束无损传输时亮度守恒关系
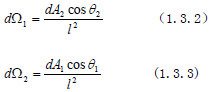
假定光束传输过程中没有吸收、反射等损失,应有:

将(1.3.2)、(1.3.3)式代入(1.3.4),得:

上式表明:如忽略传输损失,辐射源的亮度等于仪器接收端的辐亮度。如考虑传输损失,两者也仅差一个传输效率。
上述结论虽是通过一个特例导出的,实际上它反映了一个封闭光束在无损失的同种介质传输时亮度的传递关系,具有普遍的意义。不仅光束源端和接收端的亮度是相等的,在封闭光束的各个截面的亮度也处处相等,我们称之为亮度守恒定律。
由于利用辐射的一些基本定律可较为方便地求得源的辐亮度,接收辐亮度则等于源的辐亮度,或源的辐亮度乘以传输效率。知道了仪器接收的辐亮度,就不难求得辐照度和辐射功率。当测量方向与仪器光轴重合时,公式更为简洁。
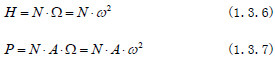
式中:Α,Ω,ω分别为仪器的入瞳面积、视场立体角和视场角。
由于Α·Ω是仪器固有的参数,只要满足面源的约定,仪器测得的辐射功率正比于源的辐亮度,而与测量距离无关。这样就可以获得真实的辐射数据。现以一个激光探测的实例说明之。
计算实例
实例:用一个10.6微米CO2激光器(15W, 出射窗¢5mm)作为光源,激光束打在墙面后漫射。用一台室温热象仪(8~14微米,120°视场,F数0.8,孔径7.1mm,320×240元)对激光散射斑成像。热象仪至墙面,激光源至墙面均为2米。
求:入射到热象仪的激光辐照度
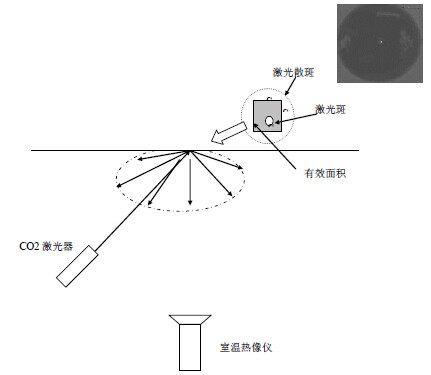
图1.8 激光散射辐射能量计算
热象仪瞬时视场
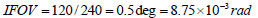
瞬时视场所张的立体角

每个像元能看到的有效辐射面积
激光斑面积
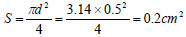
激光散射的辐射强度
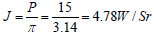
按点源公式,热象仪处辐照度
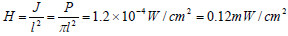
如在激光器前加凹透镜发散,束散角为1°,墙面上光斑直径约35mm,辐射源已充满瞬时视场,因此,只有部分光斑的能量能到达探测元。可先求激光散斑的辐亮度:
式中S’为发散光斑面积
再求得系统入瞳处的辐照度
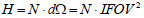
可以发现:照射在热像仪的照度与热像仪至墙的距离无关。距离增加时,每个像元能看到的有效辐射面积与距离的平方成正比,而光斑对热像仪所张的立体角与距离平方成反比,只要发散光斑还是充满像元视场,辐射面积的增加完全补偿了立体角的减小,热像仪收到的辐射通量不变,即照度不变。