黑体辐射遵循三条规律:(1)斯忒藩—波尔兹曼定律(Stefan-Boltzmann law);(2)维恩(Wien)位移定律;(3)普朗克辐射定律。
斯忒藩—波尔兹曼定律
斯忒藩—波尔兹曼定律(Stefan-Boltzmann law)是热力学中的一个著名定律。1879年约瑟福· 斯忒藩(Stefan)通过对实验数据的分析,提出了物体绝对温度为T、面积为S的表面,单位时间所辐射的能量(辐射功率或辐射能通量)M( λ,T)存在如下关系:
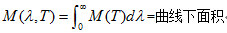
5年后,鲁德维格·波尔兹曼(Boltzmann)从理论上推导了这个公式:
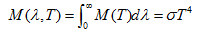 (4)
(4)
这就是斯忒藩-波尔兹曼定律。 是斯忒藩-波尔兹曼常数,是对所有物体均相同的常数。此式表明,绝对黑体的总辐出度与黑体温度的四次方成正比,即黑体的辐出度(即曲线下的面积)随温度的升高而急剧增大。
是斯忒藩-波尔兹曼常数,是对所有物体均相同的常数。此式表明,绝对黑体的总辐出度与黑体温度的四次方成正比,即黑体的辐出度(即曲线下的面积)随温度的升高而急剧增大。
由于黑体辐射是各向同性的,所以其辐射亮度L与辐射度有关系,斯忒藩—波尔兹曼定律也可以用辐射亮度表示为:
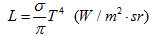 (5)
(5)
维恩(Wien)位移定律
维恩(Wien)位移定律对应一定温度T的M( λ,T)曲线有一最高点,位于波长λmax处。温度T越高,辐射最强的波长 λ越短,即从红色向蓝紫色光移动.这对于高温物体的颜色由暗红逐渐转向蓝白色的事实. 在研究工作中,可以从实验上测量不同温度下M( λ,T)曲线峰值所对应的波长λmax与温度T之间的定量关系,也可以利用经典热力学从理论上进行推导. 历史上德国物理学家维恩于1893年找到了λmax与T之间的关系如果用数学形式描述这一实验规律,则有:

即光谱亮度的最大值的波长λmax与它的绝对温度T成反比:
 (6)
(6)
这就是著名的维恩位移定律。而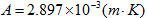 为一常数,即维恩常数。维恩因热辐射定律的发现1911年获诺贝尔物理学奖。
为一常数,即维恩常数。维恩因热辐射定律的发现1911年获诺贝尔物理学奖。
随温度的升高,绝对黑体光谱亮度的最大值的波长向短波方向移动。由于辐射光谱的性质依赖于它的温度,我们可以用分析辐射光谱的办法来估计诸如恒星或炽热的钢水等一类炽热物体的温度。热辐射是连续谱,眼睛看到的是可见光区中最强的辐射频率。某种物质在一定温度下所辐射的能量分布在光谱的各种波长上,它给人们提供了某一辐射体用作光源或加热元件的功能,但它们本身并非黑体。请注意,一般辐射源所辐射的光谱(能量按波长分布曲线)依赖于辐射源的组成成分,但对于黑体,不论它们的组成成分如何,它们在相同温度下均发出同样形式的光谱。
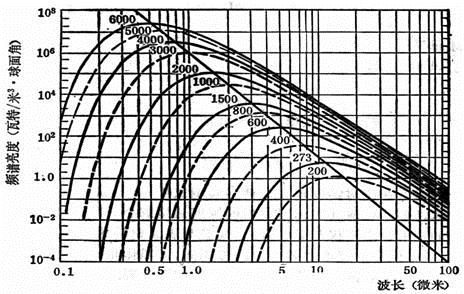
图1 黑体的频谱亮度随波长的变化关系曲线图
图1为黑体的频谱亮度随波长的变化关系曲线图。每一条曲线上都标出黑体的绝对温度。与诸曲线的最大值相交的直线表示维恩位移线。
分析图中曲线可发现该曲线有如下特征:
(1)在任何确定的温度下,黑体对不同波长的辐射本领是不同的。
(2)在某一波长λ处有极大值,说明黑体对该波长具有最大的单色辐出度。
(3)当温度升高时,极大值位置向短波方向移动,曲线向上抬高并变得更为尖锐。
小结:
以上两定律将黑体辐射的主要性质简洁而定量地表示了出来,很有实用价值。根据斯忒藩-波尔兹曼定律,热辐射能量随温度迅速增大。如果热力学温度加倍,例如从273K增到546K,辐射能量就增大16倍.因此,要达到非常高的温度,必须提供相应的能量以克服热辐射所造成的能量损失。反之,在氢弹爆炸中可以出现3×107K以上的温度,在这么高的温度下,读者可算一算,一种物质1cm2表面的能量将是该物质在室温下所固守能量的多少倍呢?
利用维恩位移定律可以测定辐射体的温度,如测定了λmax,则可得到辐射体的温度。例如太阳表面发出的辐射在0.5μm附近有一个极大值,我们可估算太阳的表面为6000K左右。还可以比较辐射体表面不同区域的颜色变化情况,来确定辐射体表面的温度分布,这种以图形表示出的热力学温度称之为热象图。热象图技术已在宇航、医学、军事等方面广为应用。如利用热象图的遥感技术可以监测森林火警,也可以用来监测人体某些部位的病变等。
黑体辐射的光谱分布—普朗克辐射定律
普朗克辐射定律为了获得绝对黑体单色辐射度的数学表达式,19世纪末许多物理学家作了巨大努力,从经典热力学、统计物理学和电磁学的基础上去寻求答案,但始终没有获得完全成功。1896年维恩根据经典热力学理论导出的公式只是在短波波长与实验曲线相符;1900--1905年瑞利(Rayleigh)和靳斯(Jeans)根据统计物理学和经典电磁学理论导出的公式只是在波长很长时不偏离实验曲线。他们的共同结论是,在波长比λmax短时,辐射能量将趋于无穷大。这显然是荒谬的结果,在物理学历史上,这一个难题被称为“紫外灾难”。“紫外灾难”表明经典物理学在解释黑体辐射的实验规律上遇到了极大的困难,是19世纪末经典物理学大厦上的两朵乌云之一。显然,如果事实不能被理论说明,那么理论存在缺陷,必须获得重建。
1900年,对热力学有长期研究的德国物理学家普朗克综合了维恩公式和瑞利—靳斯公式,利用内插法,引入了一个自己的常数,结果得到一个公式,而这个公式与实验结果精确相符,它就是普朗克公式:
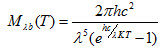 (7)
(7)
式中h为普朗克常数,c为真空中的光速,K为波尔兹曼常数,令,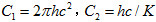 ,则(7)式可写为:
,则(7)式可写为:
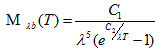 (8)
(8)
式(8) 中,第一辐射常数C1=3.7415×10-16(W·M2)
第二辐射常数C2=1.43879×10-2(M·K)
图2给出了不同温度条件下黑体的单色辐射度随波长的变化曲线。由图2可见:
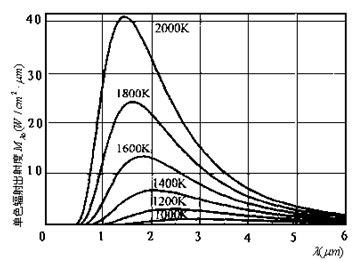
图2 黑体的单色辐射出射度的波长分布
(1)对应任一温度,单色辐射度随波长连续变化,且只有一个峰值。对应不同温度的曲线不相交。因而温度能唯一确定单色辐射出度的光谱分布和辐射出射度(即曲线下的面积)。
(2)单色辐射出射度和辐射出射度均随温度的升高而增大。
(3)单色辐射度的峰值随温度的升高向短波方向移动。
为了从理论上得出正确的辐射公式,普朗克假定物质辐射(或吸收)的能量不是连续地、而是一份一份地进行的,只能取某个最小数值的整数倍。这个最小数值就叫能量子,辐射频率为V的能量的最小数值E=hv。其中h=6.6260×10-34(J·s),普朗克当时把它叫做基本作用量子,现在叫做普朗克常数。
普朗克在物理学上最主要的成就是提出著名的普朗克辐射公式,创立能量子概念。能量子假说的提出,给经典物理学打开了一个缺口,为量子物理学安放了一块基石,宣告了量子物理学的诞生。由于这一概念的革命性和重要意义,普朗克获得了1918年诺贝尔物理学奖。
由普朗克黑体辐射公式推导出经典公式
事实上,我们不难从普朗克公式推导出经典公式。
瑞利-靳斯公式
由(8)式可以看出,当λT很大时,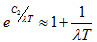 ,则可得到适合长波区域的瑞利-靳斯公式:
,则可得到适合长波区域的瑞利-靳斯公式:
 (9)
(9)
维恩公式
当λT很小时, ,则可得到适合短波区域的维恩公式:
,则可得到适合短波区域的维恩公式:
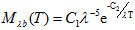 (10)
(10)
维恩位移公式
单色辐射出射度最大值对应的波长λm应由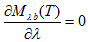 来决定。可得:
来决定。可得:
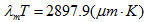 (11)
(11)
这就是著名的维恩位移公式。根据这一定律,只要知道了黑体的温度,就能直接得到黑体最大辐射出射度对应的峰值波长。
斯忒芬-波尔兹曼定律
对(8)式积分可得到黑体的辐射出射度为:
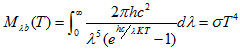 (12)
(12)
式中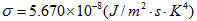 为斯忒藩——波耳兹曼常数,而(12)式就是斯忒藩——波耳兹曼定律。它表明黑体的辐射出射度只与黑体的温度有关,而与黑体的其他性质无关。
为斯忒藩——波耳兹曼常数,而(12)式就是斯忒藩——波耳兹曼定律。它表明黑体的辐射出射度只与黑体的温度有关,而与黑体的其他性质无关。